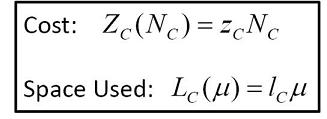- Model de trànsit macroscòpic (MFD)
- Flux de la xarxa
- Funció de sortida de la xarxa
- Costos d’un viatge en cotxe
- Corba de partença
- Autors
Contents
[hide]Model de trànsit macroscòpic (MFD)
El professor Carlos F. Daganzo és catedràtic de Ciència del Transport de la Universitat de Califòrnia, a Berkeley, on també ocupa la càtedra d’Enginyeria Civil Rober Horonjeff i el lloc de director del Centre d’Excel·lència de la Fundació Volvo sobre el Futur del Transport Urbà. Diverses de les seves aportacions han esdevingut fites en la recerca i innovació del transport: els models pròbit de demanda, el disseny de sistemes logístics i de cadenes de subministrament estables, la tarifació de congestió mixta, el diagrama fonamental macroscòpic del trànsit a les ciutats o el disseny i la gestió d’autobusos eficients, com la xarxa que es començarà a implantar aquest mateix any a Barcelona. És doctor enginyer de Camins, Canals i Ports, va rebre el doctorat a la Universitat de Michigan i també ha estat professor del MIT (Institut Tecnològic de Massachusetts).
Recentment s’ha demostrat, tant teòricament com experimentalment, que el flux mitjà i la densitat mitjana d’algunes vies de trànsit estan relacionats per una fórmula única i reproduïble: es poden modelar i formular amb l’anomenat diagrama fonamental macroscòpic (MFD). Per a xarxes en què els vehicles no poden reencaminar-se de manera adaptativa per suprimir la congestió, aquesta relació és robusta si només hi ha pocs vehicles a la xarxa. A mesura que les xarxes es van omplint de vehicles, els viatges es completen a una ràtio menor que la predita per la teoria MFD. Operar sobre aquestes xarxes en congestió causa molts efectes indesitjats, que són particularment desfavorables en xarxes compartides per múltiples modes d’operació, ja que el transport públic pateix la congestió creada per altres vehicles. Aquesta situació es produeix sobretot en ciutats on el desenvolupament de les infraestructures no ha seguit el desenvolupament econòmic.
Una manera d’incrementar l’eficiència és dedicar de manera exclusiva un espai a la carretera, més del que ocupen, per a altres modes de transport més eficients. Tot i així, la resta de l’espai s’ha de racionalitzar d’alguna manera ja que, si no, hi ha embussos.
Daganzo demostra que els modes segregats permeten a la infraestructura servir el mateix nombre de viatges per persona amb menys vehicles i sense retards. A més, demostra que això es pot aconseguir amb modes de pagament per assegurar que el comportament dels usuaris sigui el que maximitza la productivitat de la xarxa i els beneficis de tothom.
Model de trànsit macroscòpic (MFD)
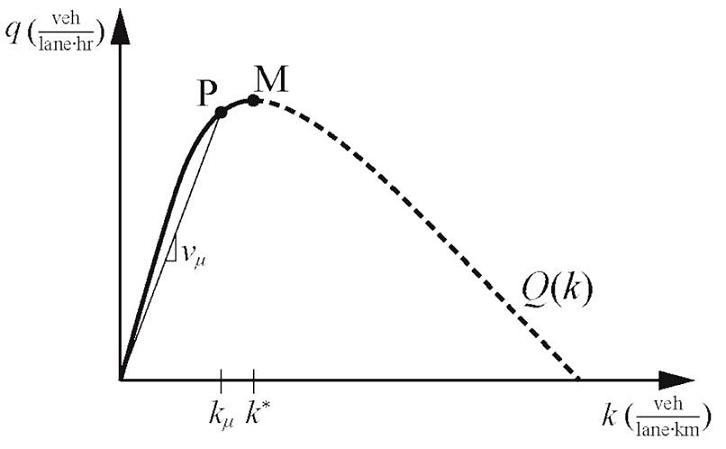
Com s’ha comentat, hi ha una relació consistent entre la densitat mitjana de vehicles a la xarxa i la mitjana del flux que s’anomena diagrama fonamental macroscòpic (MFD). Aquesta relació és una propietat de la xarxa i no depèn del patró de la demanda. Es pot modelar emprant mesuradors de flux a diferents hores i en diferents dies, i es comprova que és consistent. Així doncs, seguint aquesta funció, unes dades es poden preveure en funció de les altres.
Flux de la xarxa
El màxim flux de la xarxa s’assoleix al punt M de la figura anterior. El que és important és maximitzar la mobilitat, que és el mateix que maximitzar el flux de la xarxa. Qualsevol flux per sota del pic està associat amb dues densitats: una de més baixa que k*, i una de més alta. Aquesta darrera correspon a la línia discontínua, i és una situació en què el transit està congestionat perquè el mateix flux es podria servir amb menys vehicles a la carretera. Per tant, una xarxa ben gestionada mai no ha de permetre densitats que excedeixin k*: seria ineficient i, a més, inestable.
Investigacions recents demostren que si els conductors no escullen rutes de manera adaptativa en temps real per eliminar la congestió, les xarxes, per si soles, quan hi ha pocs vehicles, tendeixen a una distribució de vehicles uniforme; altrament, la xarxa es congestiona.
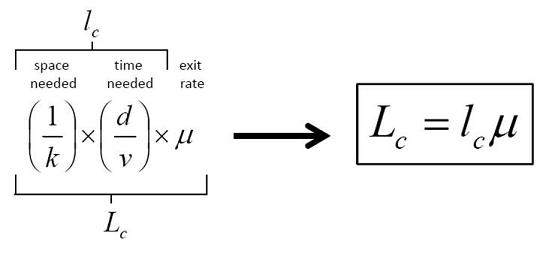
La funció de sortida de la xarxa és:
On lc és l’espai-temps consumit per un viatge de vehicle i Lc és la longitud que requereix tenir la xarxa. Per tant, amb aquestes dues dades es pot calcular la ràtio de sortida μ.
Funció de sortida de la xarxa
La funció de sortida de la xarxa és:
On lc és l’espai-temps consumit per un viatge de vehicle i Lc és la longitud que requereix tenir la xarxa. Per tant, amb aquestes dues dades es pot calcular la ràtio de sortida μ.
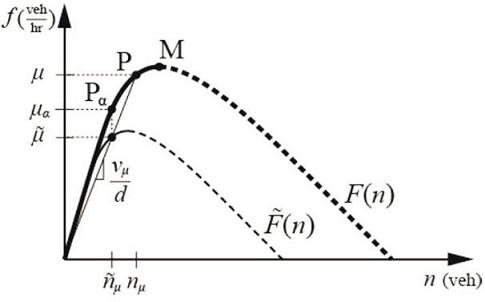
Tot i que el punt M correspon al flux més gran de sortida de vehicles possible, una ciutat pot optar per posar un límit de sortida inferior a μ associat al punt P que es troba a l’esquerra d’M, la qual cosa incrementa el temps total de viatge, ja que inclou el temps d’espera fora de la xarxa, però disminueix el temps que els vehicles són a la xarxa (μ = F(nμ)). Definim retard com l’excés del temps de viatge sobre d/vμ per a un viatge de llargada d.
Costos d’un viatge en cotxe
Hi ha molts tipus de costos associats amb el sistema de transport, que també depenen de l’estructura de la ciutat, la característica de la demanda i les propietats dels diferents modes de transport emprats i la llargada del viatge. Del que no depenen ni aquest cost ni el mínim espai requerit és, en canvi, del nombre de viatges en cotxe, NC. Així doncs, el cost total de tots els viatges en cotxe (ZC) i l’àrea total de carretera requerida per aquests cotxes (LC) són proporcionals al nombre de conductors:
Gestió del trànsit pendular (commuters)
Es proposa un model per gestionar el conjunt de desplaçaments del domicili al lloc de treball, i a l’inrevés, fets cada dia feiner pels habitants d’una àrea, l’anomenat trànsit pendular (commuters). Aquest model de gestió es fonamenta en la convivència de dos modes de transport, el vehicle privat i el transport públic, sense que el segon hagi de compartir via amb el primer, i en la regulació dels possibles embussos del mitjà privat amb taxes que penalitzin les franges temporals on es produeix un pic de densitat de trànsit.
Es fa una mesura comparativa entre el model mancat de via segregada per a transport públic i el model que sí que en té, i s’analitza si reduint la capacitat de la via que ha de servir per a la resta del trànsit millora el flux.
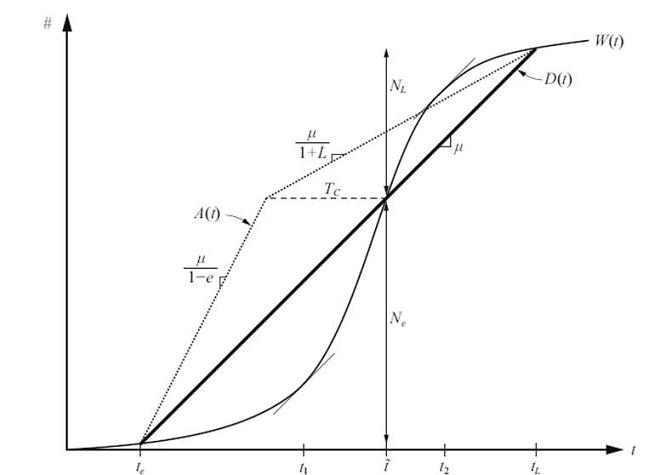
- La primera gràfica mostra l’escenari sense cap via segregada per al transport públic, s’analitza l’equilibri quan només s’empra un mode (vehicle) i una capacitat determinada. En absència d’un mode alternatiu, els viatgers arriben i surten del coll d’ampolla amb la gràfica W(t), en què D(t) és la densitat de trànsit amb pendent μ. En aquest cas, observem que només hi ha un punt on es produeix l’equilibri.
El resultat és crític quan un conductor, amb temps desitjat t, parteix del coll d’ampolla amb un retard de Tc. Ne és el nombre de conductors que surten aviat, i per tant abans de l’embús, NL els que surten tard.
Sortida i el mode de transport emprat
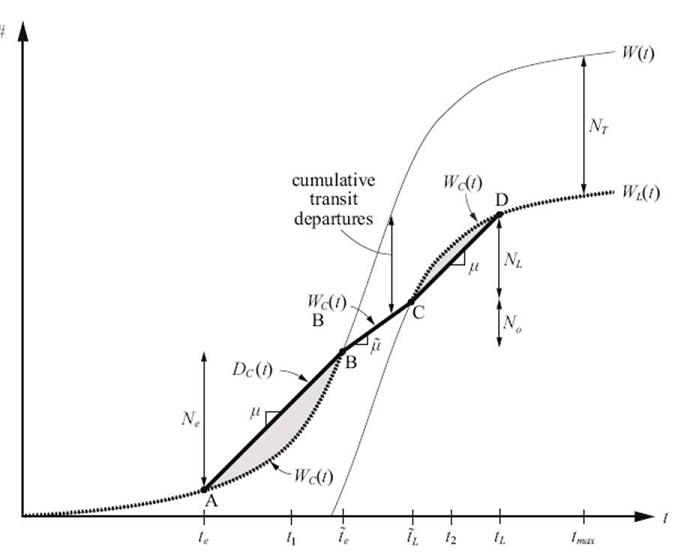
En aquest supòsit tenim dos sistemes de transport, i els viatgers de trànsit pendular poden escollir quan sortir i el mode de transport a emprar.
Com que una part de la infraestructura es dedica al mode alternatiu, la seva capacitat μ estarà afectada (per reflectir-ho emprem la constant α). Comparant les dues gràfiques s’obté que el màxim cost d’un viatge en un doble mode sempre és inferior al que es produiria amb un sol mode, ja que es redueix el nombre de viatgers que han de sortir abans i també els que arriben més tard a la destinació. El període d’embús és més curt i involucra menys conductors.'
Equilibri del sistema
Per saber com es pot assolir l’equilibri del sistema (mínim global de la diferència), cal tenir en compte si és possible arribar a una solució que tendeixi cap al punt d’equilibri. Es demostra que aquest mínim es pot assolir si l’agència de trànsit escull el camí i el mode que cal emprar per aconseguir el millor resultat global, és a dir, per minimitzar els costos temporals i econòmics. Per fer-ho n’hi ha prou d’identificar les corbes de partida per a vehicles privats i per a transport públic W(t) i establir la funció de costos econòmics (petroli, vehicles, infraestructures, etc.) i temporals (retards en l'arribada) que es vol minimitzar.
Corba de partença
Així s’obté la corba de partença per a cotxes donat el mínim retard permès. On WL(t) seria la corba de partida aconsellada per al cotxes per a un retard N(t) determinat.
El sistema també es pot regular per assolir la solució que maximitza l’equilibri, establint unes taxes per a l’ús del canal en moments en els quals es prevegi que el sistema es pugui desestabilitzar.
Daganzo ha fet també simulacions per veure si aquests resultats es poden extrapolar a xarxes que estiguin uniformement distribuïdes, o si el trànsit que transcorre per diferents canals presenta un comportament que es pugui modelar d’aquesta manera.
Vincle a un article de base
Morning Commute with Competing Modes and Distributed Demand: User Equilibrium System Optimum, and Pricing. Eric J. Gonzales and Carlos F. Daganzo. June 2011
Vincle a un article de divulgació
La Contra de la Vanguardia de l’11 d’abril de 2012
Autors
Redactat per: Marga Torre
Per saber-ne més: Francesc Soriguera