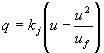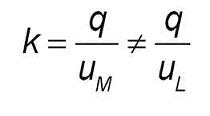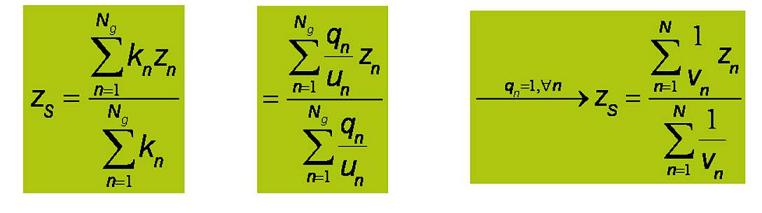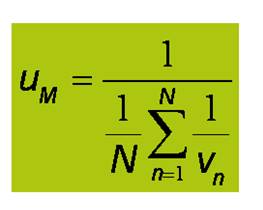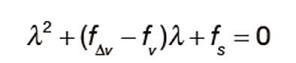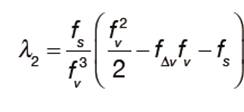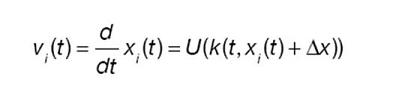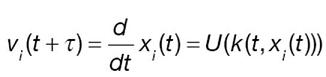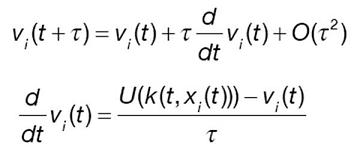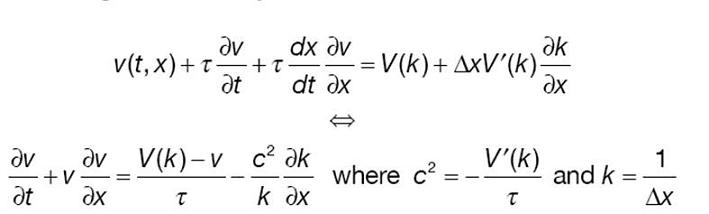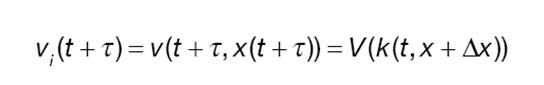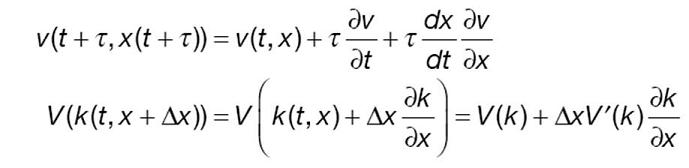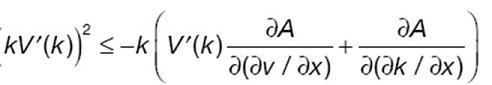Torre Thorson 2011e

• Flux de trànsit
• Alternatives
• Optimal Velocity Model (OVM)
• Multiclass macroscopic modelling
• Autors

Flux de trànsit

La gestió del flux de trànsit ha de tenir en compte que és una interacció complexa entre conductors, infraestructura i el control del seu funcionament. Així doncs, ha de gestionar complexes interaccions entre processos simples que es descriuen per cues i teories de xoc d’ones. Aquesta realitat s’intenta modelar amb diferents aproximacions. Aquest curs ha intentat donar fets empírics, teories, models i eines per interpretar, entendre i predir fenòmens relacionats amb la gestió del trànsit.

El curs va començar amb una breu presentació de les variables que interaccionen: flux, densitat, etc. i la seva representació amb una eina que ha donat suport a la major part de les teories que és el diagrama fonamental. El treball llavor dels diferents models del flux de trànsit és Greenshields 1935, del qual es deriven les equacions parabòliques per la corba velocitat/flux, basada en la relació lineal de la velocitat i la velocitat juntament amb l’equació del flux = velocitat * densitat:

  Aquest model va imperar durant cinquanta anys, tot i que presenta alguns problemes i que actualment està acceptat que és un bon model per relacionar la densitat amb la velocitat, però que no pot gestionar correctament altres característiques com: congestió homogènia, oscil·lacions de la congestió, moviment d’embussos, etc.

En aquesta relació hi intervenen variables que necessiten d’interpretació. Per exemple s’ha d’establir com es mesura la velocitat:

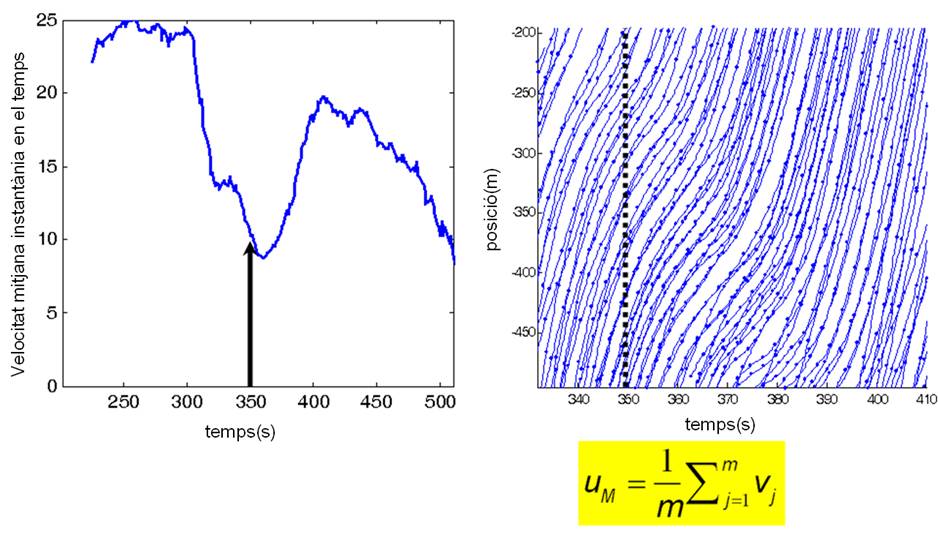
Velocitat mitjana:Es pot considerar des de dos punts de vista: l’espacial i el temporal.

  D’aquestes dues definicions es desprèn que és més representativa la velocitat mitjana espacial, ja que en el temps és esbiaixada i clarament invàlida la relació amb la densitat.

Flux = densitat de trànsit  × velocitat mitjana

i el flux derivat

   

  Aquesta mesura de velocitat es pot aproximar amb observacions locals. Per exemple es pot considerar el flux de trànsit subdividit en N_g grups homogenis de vehicles, n dels quals tenen característiques z_n. Aquestes “z_n poden ser velocitat, acceleració, edat dels conductors,nombre de rodes, pes, etc.

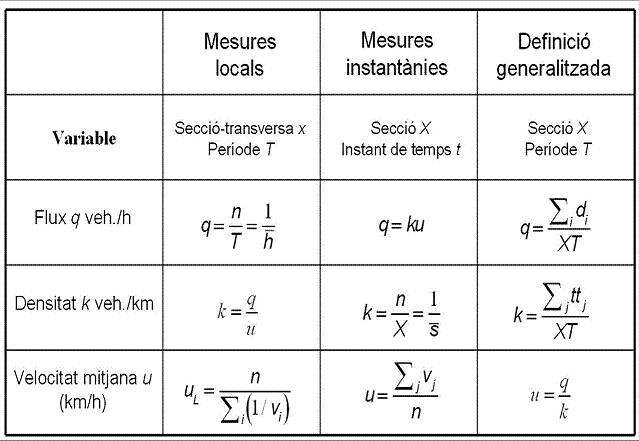
La de sota és la taula resum de les variables més emprades:

Les relacions entre les variables no impliquen causalitat, així doncs, en condicions de congestió, densitat ve determinada per la velocitat, i flux sota condicions de congestió ve determinat per densitat.I dóna lloc al primer model de treball Diagrama Fonamental

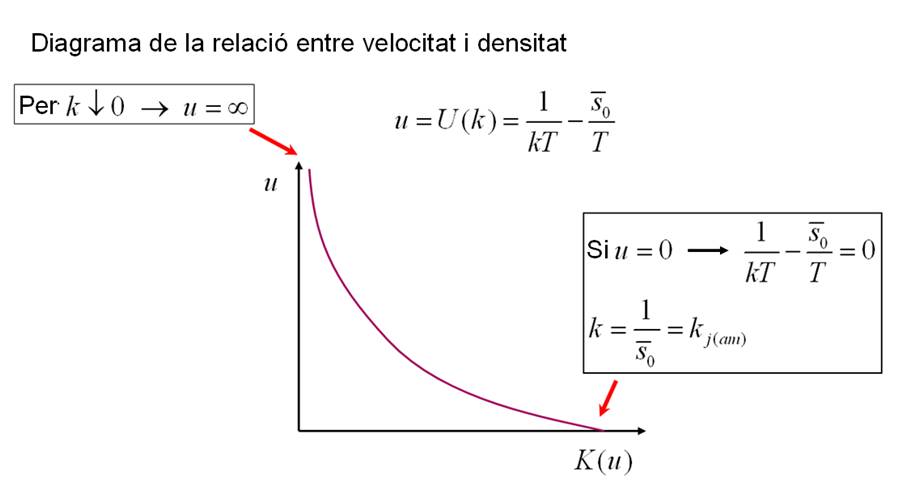
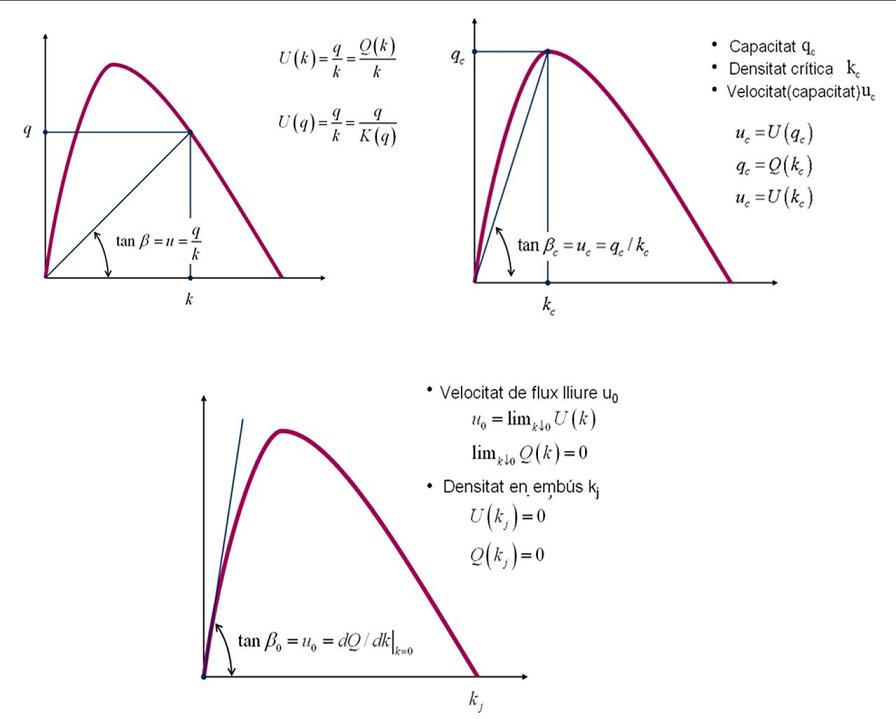
Per descriure les diferents casuístiques cal canviar les coordenades de representació:

Alternatives

La primera alternativa a aquest primer intent de modelar el flux amb el diagrama fonamental fou la teoria del trànsit en tres - fases, desenvolupat per Kerner entre el 1996 i el 2002, que està centrada en explicar la component física de col·lapse del flux i el resultat de la congestió del trànsit a les autopistes. Així doncs, mentre la teoria anterior té dues fases: flux lliure (F) i congestió de trànsit, Kerner divideix aquest darrer en dues fases: flux sincronitzat (S)i ampli embús en moviment (J).

La teoria de Kerner estableix:

• La presència de espontànies transicions entre estats, que també s’anomenen autoorganització.
• Les condicions de trànsit es divideixen en:
  • Condicions estables. Les alteracions no duen a un canvi de fase.
  • Metaestabilitat. Les petites alteracions són absorbides, mentre que les grans causen transició de fases.
  • Inestabilitat. Qualsevol alteració causa una transició de fase.

Aquesta teoria es pot recollir amb el segon model teoria de primer ordre o d’ones de xoc es donen les següents consideracions:

• Conservació de vehicles
• Tràfic funciona d’acord al diagrama fonamental q=Q(k)
• Predir com condicions no homogènies canvia al llarg del temps

Definició:

• Considerar coll d’ampolla sobre saturat (demanda > capacitat)
• Condicions de trànsit canvien al llarg de l’espai i del temps.
• Les fronteres entre les regions del trànsit es refereixen com a ones de xoc.

Aquest model és aplicable quan:

• Q(K) és coneguda per a totes les posicions,
• també es coneixen les condicions inicials, i
• es poden determinar les fronteres entre els estats.

Amb aquest model es poden representar un flux màxim a llindars de la part alta de la capacitat, sostingut al llarg d’un considerable període de temps, també recull les aturades i posades en marxa de front d’ones persistents en el temps, amb la consegüent caiguda de capacitat, fenòmens que es produeixen per avançament de vehicles més lents, i moviments dels colls d’ampolla amb espais buits per davant, així com el desplaçament d’una elevada densitat de trànsit.

Bon model per representar: amplis embussos que es van movent i que poden estar durant hores i viatjar travessant colls d’ampolla, amb una elevada densitat de trànsit en aquests embussos mòbils.

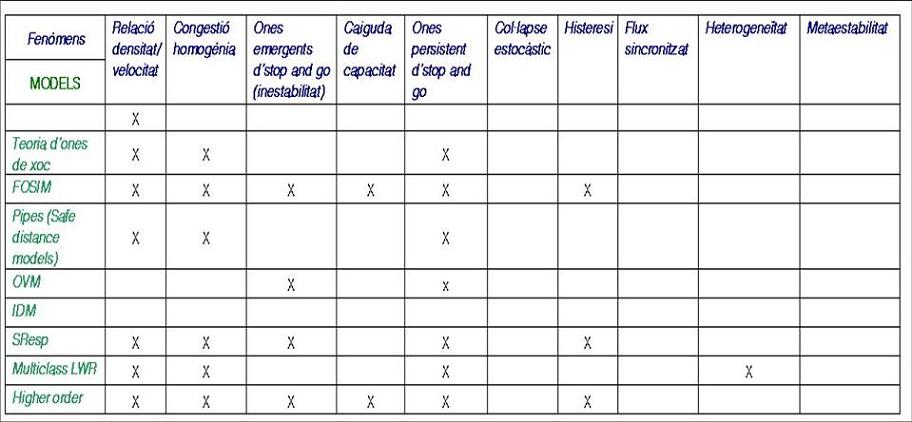
Així doncs es poden anar desgranant els diferents models que s’han aplicat a simular el trànsit, però cal fer una valoració establint tècniques i paràmetres que avaluïn la capacitat que tenen per predir el fenòmens. Així doncs,

• Es poden representar les teories de trànsit amb models i simulació?
• Realment els models prediuen els fenòmens que observem en el món real?
• Incorporen una estructura que ens permet explicar como apareixen aquests fenòmens?
• Són vàlids?

    Aquest model és aplicable quan:

• Q(K) és coneguda per a totes les posicions,
• també es coneixen les condicions inicials, i
• es poden determinar les fronteres entre els estats.

Amb aquest model es poden representar un flux màxim a llindars de la part alta de la capacitat, sostingut al llarg d’un considerable període de temps, també recull les aturades i posades en marxa de front d’ones persistents en el temps, amb la consegüent caiguda de capacitat, fenòmens que es produeixen per avançament de vehicles més lents, i moviments dels colls d’ampolla amb espais buits per davant, així com el desplaçament d’una elevada densitat de trànsit.

Bon model per representar: amplis embussos que es van movent i que poden estar durant hores i viatjar travessant colls d’ampolla, amb una elevada densitat de trànsit en aquests embussos mòbils.

Així doncs es poden anar desgranant els diferents models que s’han aplicat a simular el trànsit, però cal fer una valoració establint tècniques i paràmetres que avaluïn la capacitat que tenen per predir el fenòmens. Així doncs,

• Es poden representar les teories de trànsit amb models i simulació?
• Realment els models prediuen els fenòmens que observem en el món real?
• Incorporen una estructura que ens permet explicar como apareixen aquests fenòmens?
• Són vàlids?

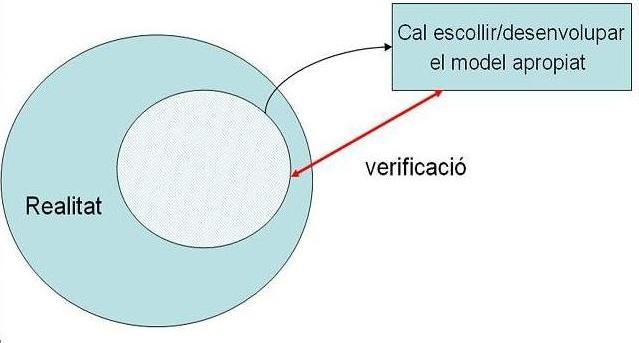
  El primer model de comprovació:

  La primera analogia que es presenta en el cas del trànsit és models continus macroscòpics tenen analogia amb models dinàmics del fluids. Però:

• El fluids són continus: hi ha moltes més molècules en una ampolla que vehicles en el món, aleshores les variables mitjanes han de tractar-se diferent. Així doncs, fora possible que de facto s’hagués de tractar el trànsit com un procés discret.
• La mida dels elements també importa: així els cotxes tenen una sèrie de paràmetres a considerar en cues, en situacions d’inèrcies, etc., que no cal considerar en les molècules.
• Els vehicles responen a estímuls, el seu comportament no és tan anisotropic com els del fluids. Per exemple, el vehicles defugen de les col·lisions.

Tot i així, models macroscòpics continus i simples són normalment millor en predir dinàmiques de trànsit a les autopistes, que d’altres complexos micromodels.

Segon model

 

  Aquestes dues fases poden implicar un gran nombre de variables desconegudes. Per determinar aquestes variables cal un gran nombre d’observacions. Per ajustar models microscòpics calen moltes trajectòries de vehicles que provinguin d’una amplia distribució de vehicles sota un ampli rang de circumstàncies.

Tercer model

File:Draft Garcia 762320368-DGC-El-fenomen-del-flux-de-tran-dgcN noticia 6 imatge 13.jpg

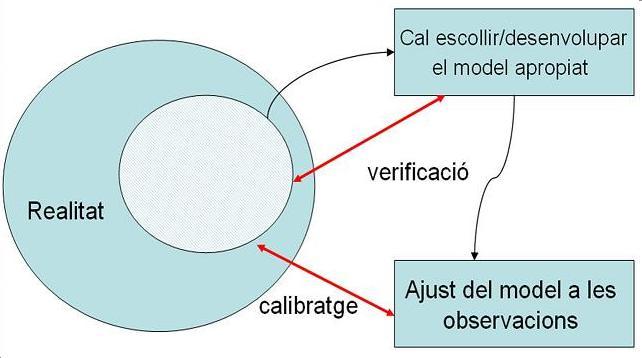
La validació comença amb el calibratge, i segueix els principis:

• Navalla d’Ockham: si els dos models tenen uns resultats igualment bons, cal escollir el model més simple.
• Penalització d’excés de paràmetres en la funció, emprar validació creuada.

  Models de seguiment de cotxes (car-following models)

Amb aquests models s’han de recollir comportaments longitudinals, laterals i creuats dels cotxes. En aquest cas l’acceleració depèn de la velocitat dels vehicle, de la velocitat, acceleració i distància al vehicle anterior. Els models analitzats han estat:

• Distància de seguretat (estàtics)
• Velocitat òptima i generalitzacions (dinàmics continus)
• Estímul-resposta (retardat i de dinàmica continuada)
• Punts d’acció (dinàmics basats en esdeveniments)

 

Safe distance Model (Pipes)

Assumim un temps de reacció del conductor, que vindrà determinat per la distància que li cal al conductor mantenir per poder aturar-se a una determinada distància del cotxe anterior, quan aquest s’atura a distància L. Seguint aquest principi es determina el diagrama fonamental.

Alpha expressa la actitud davant el risc, canvi relatiu de paràmetres

Optimal Velocity Model (OVM)

La principal assumpció és que: el conductor vol conduir a una velocitat òptima, que és una funció de la distància, en cada moment, entre el cotxe anterior i el posterior. I hi ha una simple relació:acceleració a(t) del cotxe que segueix, és una diferència entre velocitat òptima i actual velocitat. Aquest model pot predir inestabilitats de trànsit, així com la presència d’amplis moviments d’embussos i ones d’arrencada i aturada.

Stimulous response model (SResp)

La base del model és:

Resposta (t+Tau) = sensitivitat (t) x estímul (Tau)

on: resposta és acceleració (o desceleració) del següent vehicle, amb possible retard, temps de reacció (tau), sensitivitat és una funció o un paràmetre, i estímul és la distància o la diferència de velocitat entre vehicles successius.

En aquest context de models, molts autors han suggerit que el comportament d’un conductor no es pot descriure adientment només tenint en compte el comportament del vehicle que va davant; per aquest motiu s’han desenvolupat models multianticipatius de seguiment de cotxes.

FOSIM

A la universitat TU de Delft s’ha desenvolupat un model de simulació microscòpica que és una interacció simple d’un model de seguiment de cotxes basat en el model de Wiedemann i calibrat per les dades d’Holanda i amb capacitat per reproduir diferents tipus de discontinuïtats.

Per validar el models s’ha de comprovar:

• Si el model produeix relacions d’equilibri i quines són.
• Algunes de les propietats dinàmiques més sensibles.

  També s’ha de validar l’estabilitat

• global del model, que significa que petites alteracions es calmen amb el temps, és a dir que el sistema recupera la normalitat amb el temps.
• lineal, que valora como les interrupcions creixen en arribar a la secció que determina l’inici de l’embús.

  Funcionalment, es tradueix a:

• passar el model a la forma estandarditzada: a=f(s,deltav,v),
• calcular i comprovar les condicions d’equilibri. Estabilitat local amb el valor propis de l’equació següent:

 

  el signe de la part real de les arrels d’aquesta equació ens determina si hi ha o no estabilitat local.

 

• per calcular l’estabilitat lineal cal analitzar

 

Multiclass macroscopic modelling

En aquests models s’intenta tenir en compte factors diversos:

Heterogeneïtat manega una àmplia distribució de factors d’entre els qual destaquem: temps d’avenç, espais buits, característiques de vehicles, velocitats desitjades, carga de la carretera i comportament de seguiment de cotxes. L’heterogeneïtat explica part de la dispersió en el diagrama fonamental.

En tots els models macroscòpics s’ha de fer la consideració del sistema de referència de treball, ja que determinarà la capacitat dels models per tractar certs fenòmens. Així doncs, distingim dos casos:

Sistemes de coordenades eulerià: espai i temps (x,t). En altres paraules, es fa el seguiment de nombre de vehicles per metres de carretera.

Sistema de coordenades lagrangià: número de vehicle, temps (n,t). O equivalentment, es fa el seguiment d’espai, metres, per nombre de vehicles.

El sistema lagrangià proporciona certes avantatges:

1. En el sistema eulerià les solucions numèriques són altament no lineals, hi ha moltes oscil·lacions entre estats: congestió de trànsit o de trànsit. En aquest sistemes la difusió té un paper molt important. D’altra banda en els sistema lagrangià la solució numèrica és simple i la difusió pràcticament no hi té paper.

1. Amb la idea de corregir prediccions de models amb les dades disponibles i resoldre les estimacions de estat no lineals amb l’Extended Kalman Filter:

  Factor de correcció = sensitivity model * incertesa de predicció de models/dades d’incertesa

El terme sensitivity de model en el cas de sistema de referència lagrangià és més ajustat.

1. És el pont natural entre el micro i la macro modelatge.

També hi ha desavantatges que proporcionen reptes a solucionar:

1. En el sistema lagrangià l’observador es mou amb el tràfic, això implica que la infraestructura es mou en relació amb el flux de trànsit.
2. El model de multiclass és més difícil que l’Eulerian en particular per les discontinuïtats – obres – i per incloure dades de sensor fixats.
3. El programari de simulació també és més complex i difícil d’entendre.

Un model macroscòpic en coordenades lagrangianes calcula l’espai per dn vehicles. Quan dn=1, és el micromodel més simple possible: Newell car following model.

Models de High-order

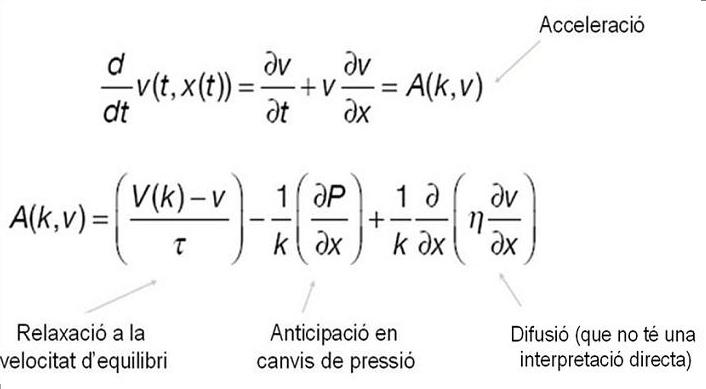
En aquest cas s’elimina l’assumpció que la velocitat dels conductors està en equilibri, tot al contrari s’assumeix que els conductors s’anticipen en condicions de trànsit dens.

Emprem el desenvolupament de Taylor per obtenir l’aproximació:

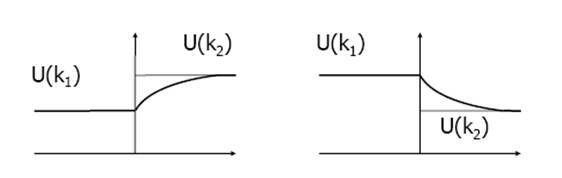
En aquests models es poden introduir la histèresis, que és anticipació a la fase més amplia. En cas de reacció, a la fase dominant (reacció retardada), la velocitat es relaxa exponencialment a una velocitat d’equilibri. Canvi abrupte de k₁ a k₂  (ona de xoc) en t=0.

Acceleració retardada, una reacció en tems Tau:

Emprant altre cop desenvolupament de Taylor:

Si incloem altres termes per elevar la representativitat del model i poder incloure tant l’anticipació com el retard, per tant d’histèresi totalment, tenim:

Si combinem les dues coses:

Un altre cop i gràcies a Taylor:

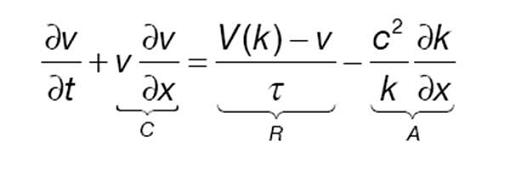
Descriptivament, i que reflexa els orígens dels models:

C: Convecció

R: Relaxació

A: Anticipació

Quines mancances hi ha amb el model de primer ordre?

• La relació estacionaria entre densitat i velocitat implica que la velocitat mitjana s’adapta instantàneament a la densitat de trànsit.
• Solucions discontinues que no es corresponen amb la “suavitat” de les condicions inicials.
• I en relació amb la gestió del flux de trànsit, el model no pot recollir:
  • Aparició d’ones d’start-top ni els embussos fantasmes.
  • El fenomen d’histèresi del trànsit i la caiguda de capacitat.

El principal problema dels models d’ordre més gran que ú, és l’estabilitat. L’anàlisi de l’estabilitat lineal determina les condicions en què aquests models es poden emprar.

Així doncs, en el cas d’un model de segon ordre:

 

és estable si:

Tot i això, els models d’ordre superior a ú, no són anisòtrops i les petites distorsions que en els models de primer ordre estan sobre una ona cinemàtica, a segon ordre estan a dos, per tant s’han de gestionar, a més, les interaccions entre elles. Així doncs, les teories recents aposten per extensions de models de primer ordre.

Autors

Redactat per: Marga Torre i Leif Thorson

Per saber-ne més: Leif Thorson