- Context
- L’estructura completa del model ADT proposat
- Primer experiment
- Exemple de gràfics de densitat-flux obtinguts
- Segon experiment
- Tercer experiment
- Benchmark vs. Model proposat
- Validació
- Autors
Contents
[hide]Context
En els darrers anys, els problemes del trànsit urbà han situat les àrees metropolitanes en una situació difícil pel que fa a la congestió i a la contaminació. Problema que s’ha vist accentuat pel fet que gran part del trànsit es canalitza pels modes de transport per carretera. A més, el temps que les persones usuàries perden en els desplaçaments té un fort impacte econòmic, per la qual cosa la planificació del transport es torna molt rellevant.
Els models matemàtics són un gran ajut ja que enriqueixen les decisions dels gestors del trànsit. En particular, aquells que s’empren per a la predicció, com per exemple els models d’assignació dinàmica del trànsit (ADT) que donen una representació temporal coherent de les interaccions entre eleccions de trànsit, fluxos i mesures de temps i de cost. Aquests models han tingut un gran desenvolupament en els darrers vint anys per causa de l’aparició de sistemes intel·ligents de transport. Aquesta tesi se centra en analitzar aquests models, per tal de millorar la resolució del problema d’acord amb un nou model ADT.
El model ADT desenvolupat en aquesta tesi està basat en una hipòtesi de comportament dels conductors al llarg del viatge que és una extensió dinàmica del primer principi de Wardrop anomenada equilibri dinàmic d’usuari (EDU) que fonamenta: “per a cada par origen-destí per a cada instant de temps, si els temps de viatge de tots els usuaris que han partit en aquest interval de temps són iguals i mínims, aleshores el flux dinàmic de trànsit a la xarxa es troba en un estat de EDU (Ran and Boyce (1996)”. Per aconseguir aquest equilibri es resol una formulació de desigualtats variacionals mitjançant un enfocament preventiu basat en un algorisme iteratiu que és una modificació del mètode de les mitjanes successives proposat per Sheffi.
L'algorisme proposat itera entre dues components principals fins que se satisfà un criteri de convergència. Aquestes dues components són:
- Un nou mètode per determinar els nous fluxos (que depenen del temps) en els camins, mitjançant els temps de viatge experimentats en aquests camins en la iteració prèvia.
- Un procediment de càrrega dinàmica de la xarxa (CDR) que determini com aquests fluxos es propaguen mitjançant els corresponents camins.
Els models DTA basats en la simulació utilitzen un simulador de trànsit per reproduir les complexes dinàmiques del flux de trànsit a la component CDR. En aquest cas, es volia poder reproduir diferents classes de vehicles, controls semafòrics i canvis de carril. Per tant, un dels objectius de la tesi ha estat desenvolupar un nou model mesoscòpic de simulació de trànsit amb aquestes característiques: multiclasse i multicarril.
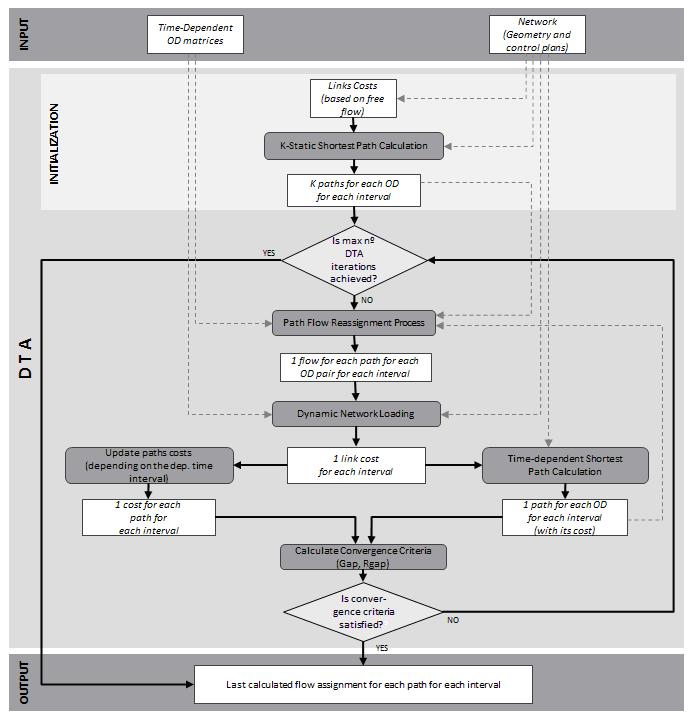
L’estructura completa del model ADT proposat
Figura 1: Estructura del model ADT desenvolupat
Primer experiment
Es pot observar que l’esquema ADT proposat inclou un component que calcula el millor camí amb costos dependents del temps, per afegir nous camins al llarg del procediment quan sigui necessari. D'altra banda, el procés pot començar amb un camí inicial determinat a través d’un càlcul estàtic del camí millor, que utilitza com a costos els que corresponen al trànsit en condicions de trànsit fluid. Després de la primera iteració, el conjunt de camins pot canviar si hi ha un camí millor, com a conseqüència dels nous costos. Així, en el procés de reassignació del flux pel camí proposat, cal tenir en compte per a aquest nou camí la seva distribució de demanda.
Per tal de validar correctament el model ADT desenvolupat, aquesta tesi proposa una validació independent de cadascun dels components principals i una validació final del model ADT complet.
Per tal de validar el procediment de reassignació de flux de forma independent del simulador, es va utilitzar el mateix esquema ADT substituint el simulador desenvolupat per un simulador de programari lliure disponible anomenat MEZZO (Burghout, 2004). Els resultats van demostrar la importància de la consistència dels resultats dels temps de viatge calculats en la part de simulació del procés global.
En el cas del simulador desenvolupat per a la component CDR es van proposar diferents experiències computacionals els resultats dels quals van demostrar el bon comportamente del simulador mesoscòpic desenvolupat.
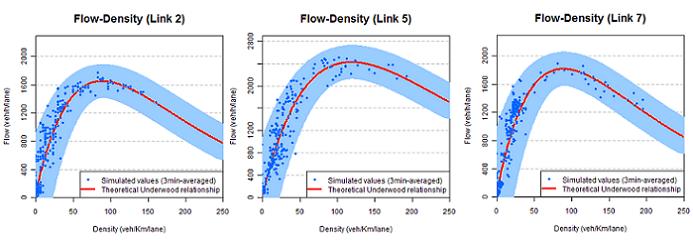
El primer experiment investiga la relació entre els valors del flux i la densitat simulada pel model proposat. Amb aquest objectiu, es fa una comparació gràfica d’aquests resultats amb els obtinguts per la teoria macroscòpica proposada per Underwood (1961). Els resultats mostren que el model desenvolupat és capaç de reproduir el diagrama fonamental del trànsit.
Exemple de gràfics de densitat-flux obtinguts
Figura 2. Exemple de gràfics de densitat-flux obtinguts
Segon experiment
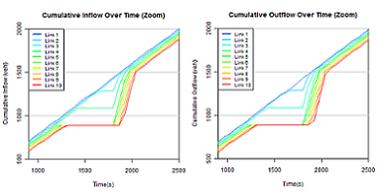
El propòsit del segon experiment fou demostrar que aquest model propaga la congestió de manera adient. Els resultats demostren que així ho fa el model i que permet la localització correcta tant pel que fa al temps com a la localització de la congestió.
Figura 3. Flux entrant i sortint als arcs de la xarxa en un experiment amb incident
Tercer experiment
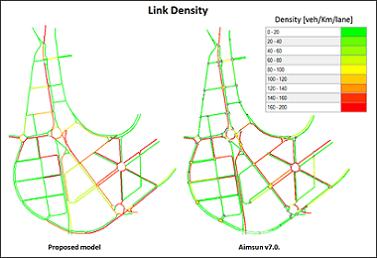
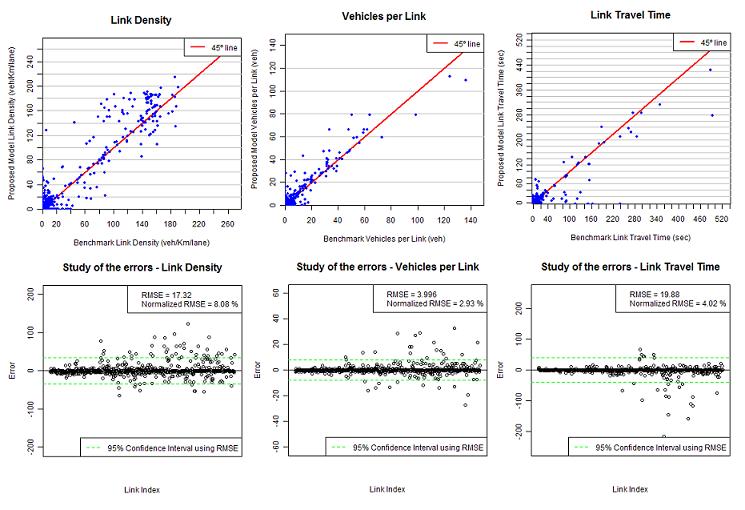
En el darrer experiment, les proves s’han fet sobre dos casos reals per provar com s’aproxima satisfactòriament el model a la realitat en què, tot i faltar dades, es van substituir per valors simulats amb un microsimulador de trànsit (Aimsun). Els resultats demostren la capacitat per reproduir comportaments multicarril i multitemporals en xarxes urbanes de mida mitjana.
Figura 4. Mitjanes de densitat a les secciones d’una xarxa al final de la simulació
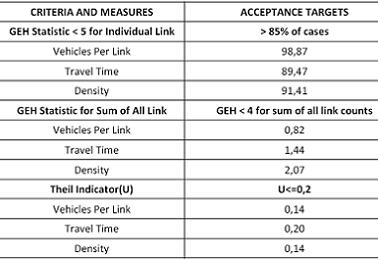
Taula 1 Resultats de mesures GEH i indicador de Theil.
Benchmark vs. Model proposat
Figura 5: Densitat a les seccions de la xarxa: benchmark vs. model proposat.
Validació
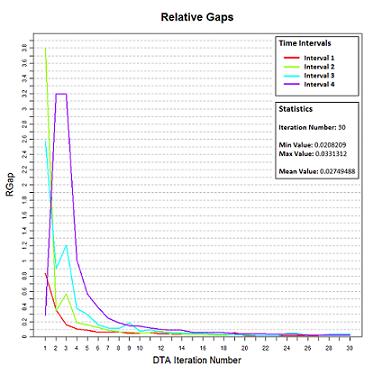
Per acabar, es va validar el model ADT mitjançant experiments sintètics realitzats sobre un escenari urbà real. Els resultats obtinguts mostren la capacitat del model ADT d’assolir un estat EDU mesurat en termes d’una funció de gap relatiu separada per interval de temps de sortida.
Figura 6. Exemple de resultats de gaps relatius dependents dels intervals obtinguts
Autors
Redactat per: Mari Paz Linares i Marga Torre. Per saber-ne més: Mari Paz Linares