Calvino et al 2014a

• Model d'assignació del trànsit percentil
• Model d'assignació de trànsit que inclou avançaments
• Model bayesià d'estimació de matrius
• Autors

Model d'assignació del trànsit percentil

El procés de planificació i avaluació dels sistemes de trànsit demana eines que siguin capaces de reproduir la realitat. Per aquest motiu, s’han desenvolupat en els darrers anys múltiples models d’eines estadístiques i matemàtiques que, a més, proporcionen resultats fàcils d’interpretar.

Les aportacions de la tesi en aquesta matèria han estat les següents:

Model d’assignació del trànsit percentil

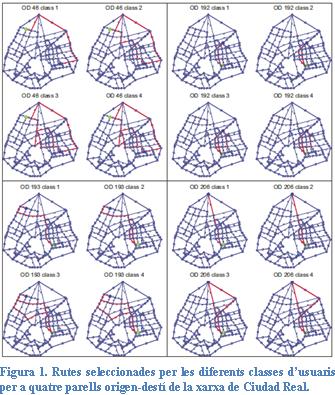
En contraposició a la majoria dels models que exigeixen enumeració de rutes, en la tesi es presenta un model d’assignació de trànsit percentil, que d’acord amb un problema d’optimació, inclou dues versions amb i sense enumeració de rutes que permeten obtenir els fluxos i els temps de viatge de les rutes seleccionades per les persones usuàries que viatgen des d’un determinat nus d’origen fins a un nus de destí (vegeu la figura 1). Aquest model es pot considerar com un model de fiabilitat del temps de viatge, ja que assumeix l’existència de classes d’usuaris/usuàries segons el seu ànim de puntualitat.

Un model d’assignació de trànsit que inclou avançaments

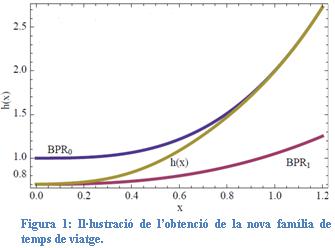
Per poder reproduir els avançaments a escala macroscòpica, en aquesta tesi es proposa una nova família de funcions de temps de viatge que proporciona diferents temps de viatge per a usuaris/àries de diferents classes quan el grau de congestió es baix i reprodueix el fet que amb la congestió alta l’avançament és impossible. Aquest conjunt de funcions està basat en combinacions lineals convexes d’altres funcions de temps de viatge.

L’autora proposa dos problemes d’optimització equivalents (amb i sense enumeració de rutes) basats en una funció de discrepància, que es poden resoldre amb programes generals d’optimització. Per demostrar el seu funcionament, s’apliquen sobre diferents conjunts de dades, incloent la xarxa real de Ciudad Real (Espanya).

Un model bayesià d’estimació de matrius

Es proposa un mètode bayesià per estimar matrius origen-destí segons les dades d’aforaments de transit. El mètode es pot considerar como un model jeràrquic de optimització ja que es resolt com un sistema d’equacions en què tres de les quals són, al seu torn, problemes d’optimització:

• Un model de Wardrop de mínima variància, que s’utilitza per determinar les proporcions d’elecció de les rutes.
• Un problema de mínims quadrats, que té per resultat la mostra de fluxos dels parells origen-destí.
• Un problema de màxima versemblança per estimar els paràmetres a posteriori.

Per resoldre el problema d’optimització, es proposa un enfocament iteratiu que proporciona la solució en poques iteracions pels exemples resolts.

Límit superior del nombre de sensors necessari per a la total observabilitat dels fluxos dels arcs d’una xarxa

La determinació del nombre mínim de sensors necessari per a l’observabilitat total dels fluxos dels arcs d’una xarxa és molt important, ja que l’observació de més arcs dels que són estrictament necessaris pot provocar problemes de redundància i, fins i tot, incompatibilitat. En la tesi es demostra que aquesta dada només es pot obtenir si es té informació sobre les rutes, tot i que no és necessària la seva completa enumeració. També es proposa un algorisme per obtenir conjunt de rutes linealment independents.

Un model pel problema dinàmic de recàrrega de xarxa incloent avançaments

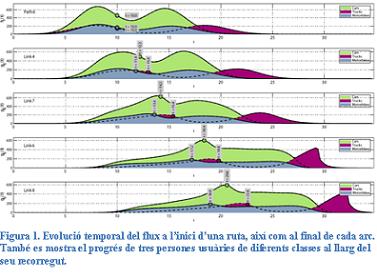
A la tesi es presenta un model per resoldre el problema dinàmic de recàrrega de xarxa quan s’assumeixen diferents tipus d’usuaris segons la seva tendència a l’avançament. El model calcula les funcions de temps de viatge en els arcs en un conjunt finit de instants igualment espaiats que s’empren per interpolar els temps de viatge a la resta d’instants. A més considera funcions de temps de viatge no lineals en els arcs que depenen del flux en el mateix arc, així com dels arcs aigües avall i pren com a hipòtesi que els temps de viatges (i, per tant, les velocitats) han de coincidir per a totes les classes en presència d’elevades congestions. Segons els temps de viatge, juntament amb altres hipòtesis, s’obté l’evolució temporal del flux dels diferents elements (arcs, nodes, etc.).

Autors

Redactat per: Aida Calviño Martínez i Marga Torre. Per saber-ne més: Aida Calviño Martínez